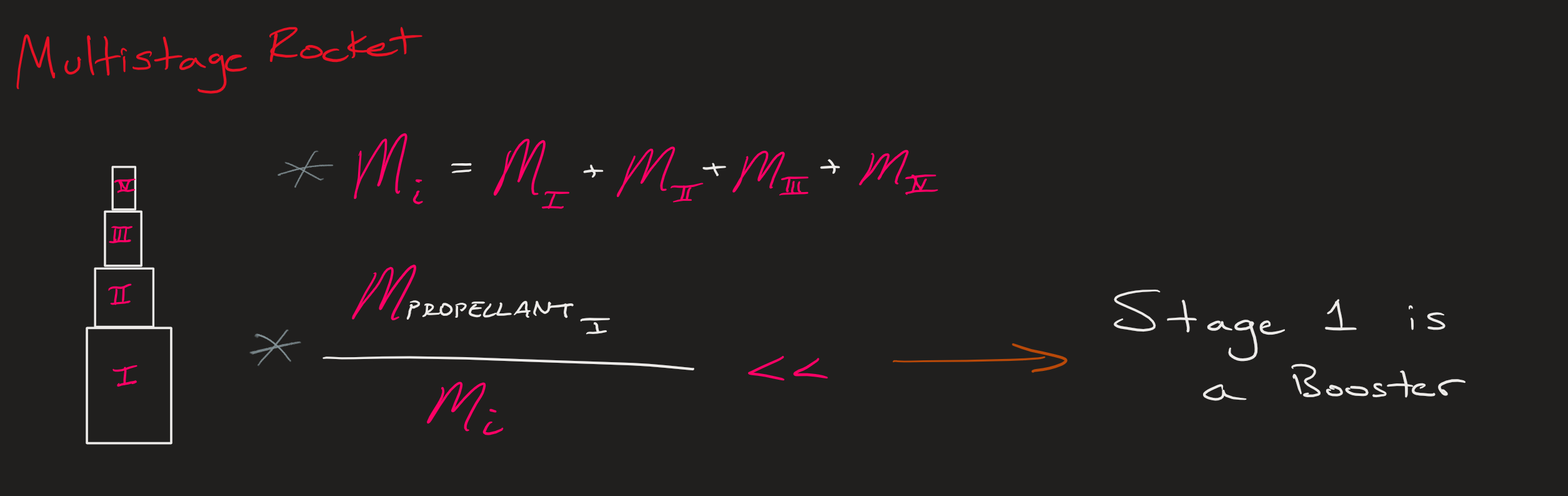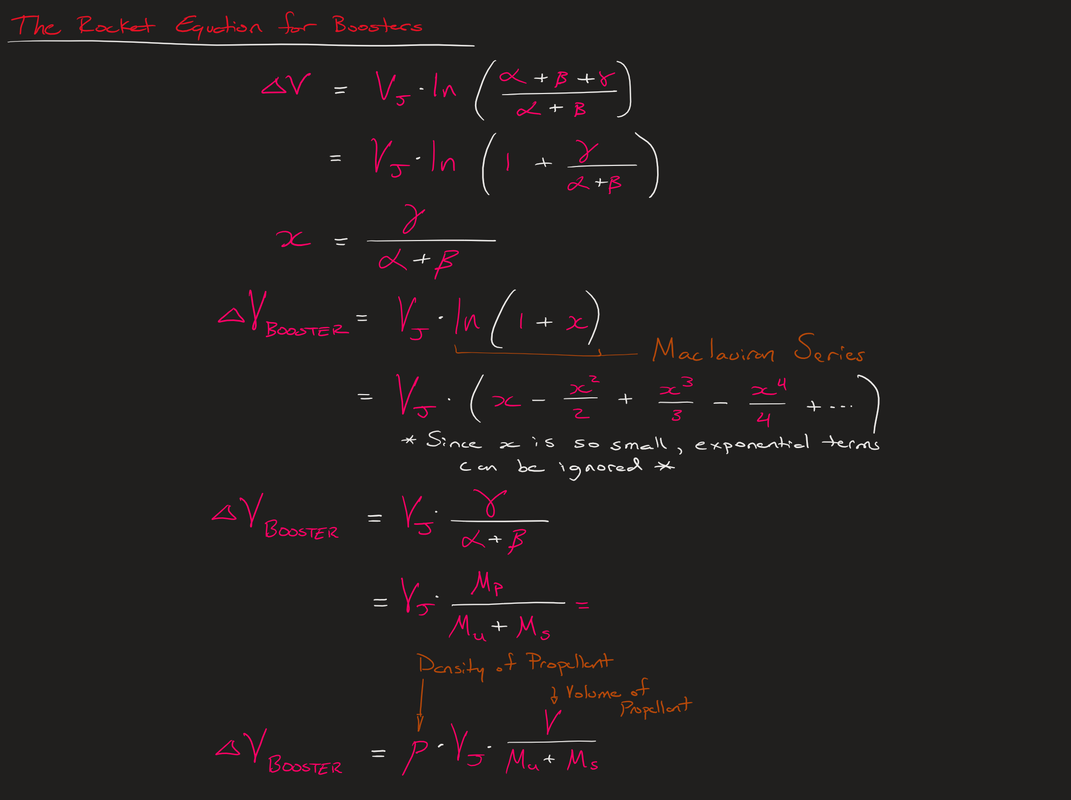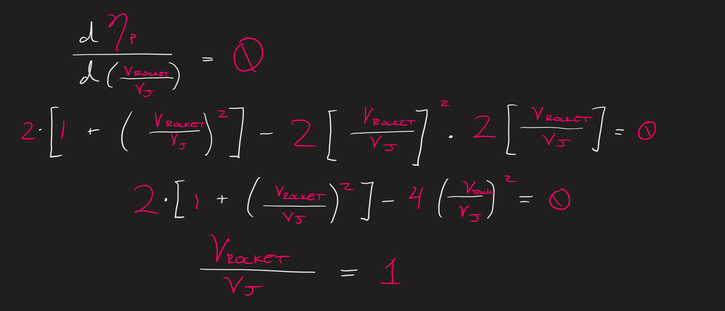L5: Propulsion Efficiency
The Booster Stage
From what we have discussed so far we understand the mass factions of a rocket and how they affect the change in velocity of the rocket. What we have yet to discuss is the acceleration of a rocket which would allow us to understand why clustering is needed on multistage rockets. Here is how you calculate the initial acceleration of the rocket.
From what we have discussed so far we understand the mass factions of a rocket and how they affect the change in velocity of the rocket. What we have yet to discuss is the acceleration of a rocket which would allow us to understand why clustering is needed on multistage rockets. Here is how you calculate the initial acceleration of the rocket.
Thus, from this equation you can see if mi is too high the acceleration will be far too slow to lift the rocket to the target altitude before all the fuel is emptied from the propellant tank. Now that we understand how to calculate the acceleration of the rocket, let's take a look one special stage of multistage rockets, known as the booster. Before we get into the real nitty-gritty of why boosters are an interesting special case of the rocket equation, let's first look at a smaller scale of a firework.
Although very small, a firework is still considered a rocket. If we were to calculate the mass fraction of the firework in terms of payload (in a firework there is no payload), a small amount of black powder, and the rest of the structure (paper, stick, fuse wire, ect.) we could find that the mass fraction of the propulsion is extremely small compared to the structure. This brings us to the concept of a booster. A booster as we will define is any case of a multistage rocket in which the mass of the propellant in the first stage divided by the mass of the whole rocket is a very small value, as shown below:
Now that we know what a booster is, would it be possible to simplify the rocket equation for boosters? Yes we can:
As you can see from the equation above, the change in velocity of a booster is a bit different from the normal rocket equation. This is because of the new terms that are being substituted for the mass of the propellant, the Volume of the Propellant, and the Density of the Propellant. This is so important since it also gives logic to the reason why boosters are composed of solid or hybrid rocket engines in which the fuel is much more dense than most cryogenic fuels such as hydrogen. Since the density is higher the ideal velocity increment is much higher.
In the world of multistage rockets it can seem quite deceptive that one could simply connect together infinite stages for whatever the desired velocity is, and be able to attain it. However, rockets get much more complicated for each stage that is added due to more sequenced stage separation which leads to more areas that are prone to failure. The most common amount of stages now a days is 2 stage to orbit, but some are still in active pursuit of achieving single stage to orbit.
Propulsion Efficiency
From what we have learned so far, how can we categorize the efficiency of our rocket? We can do that by using the following equation of propulsion efficiency (ηp):
From what we have learned so far, how can we categorize the efficiency of our rocket? We can do that by using the following equation of propulsion efficiency (ηp):
ηp = (Work Done by Rocket per Unit of Time) / (Work Done by Rocket per Unit of Time + Work Wasted)
- Work Done by Rocket = Fthrust x Distance
- = (ṁ x Vj) x L
- Work Done by Rocket Per Unit of Time = (ṁ x Vj) x L/t
- = (ṁ x Vj) x Vrocket [Watts]
- Work Wasted by Rocket
- This comes from the plume of exhaust gas that travels at the velocity: Vrocket - Vj
- = 1/2 x ṁ x (Vrocket - Vj)^2 [Watts]
ηp = ((ṁ x Vj) x Vrocket) / ((ṁ x Vj) x Vrocket + 1/2 x ṁ x (Vrocket - Vj)^2)
After simplification...
ηp = (2 x Vrocket / Vj) / (1 + (Vrocket / Vj)^2)
After simplification...
ηp = (2 x Vrocket / Vj) / (1 + (Vrocket / Vj)^2)
So given this equation above, how can we calculate the maximum efficiency of our rocket? If you derive the equation above in terms of Vrocket / Vj you will find this:
From what the equation above tells us, is that when the velocity of the rocket is equal to the velocity of the mass being ejected from the nozzle, only then is the efficiency at its maximum. This means that at this velocity once the mass of the propellant is ejected from the vehicle is has zero velocity, and thus no energy lost, this is the most ideal case, but very unlikely to occur.
Application Example #1: [Attempt this yourself before looking at the solution]
Calculate the diameter of the hole of the water bottle so that the acceleration of the bottle rocket is 0.5g. Here are your givens:
Calculate the diameter of the hole of the water bottle so that the acceleration of the bottle rocket is 0.5g. Here are your givens: