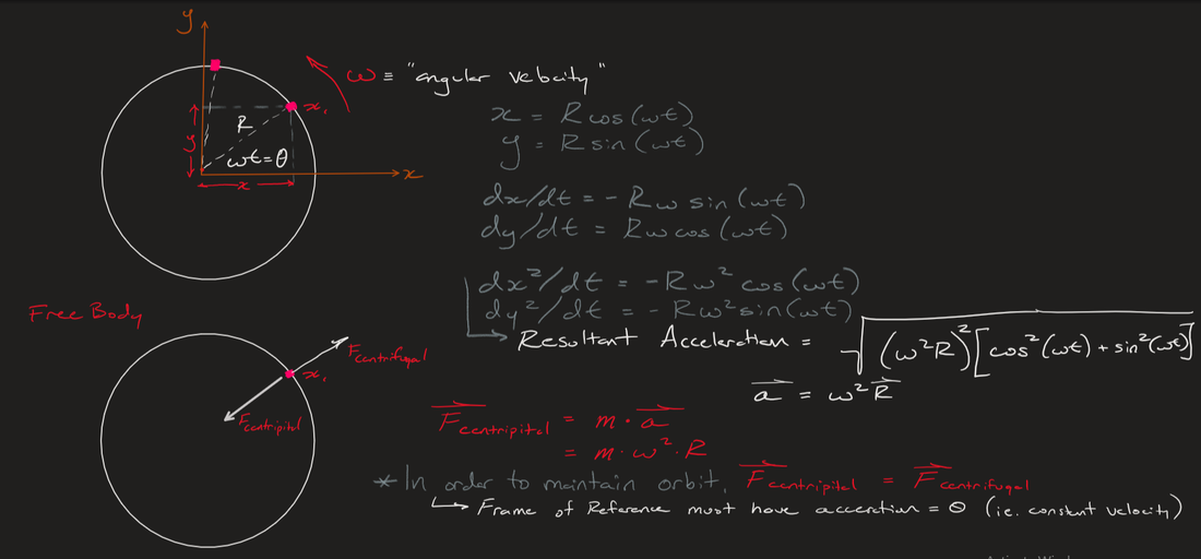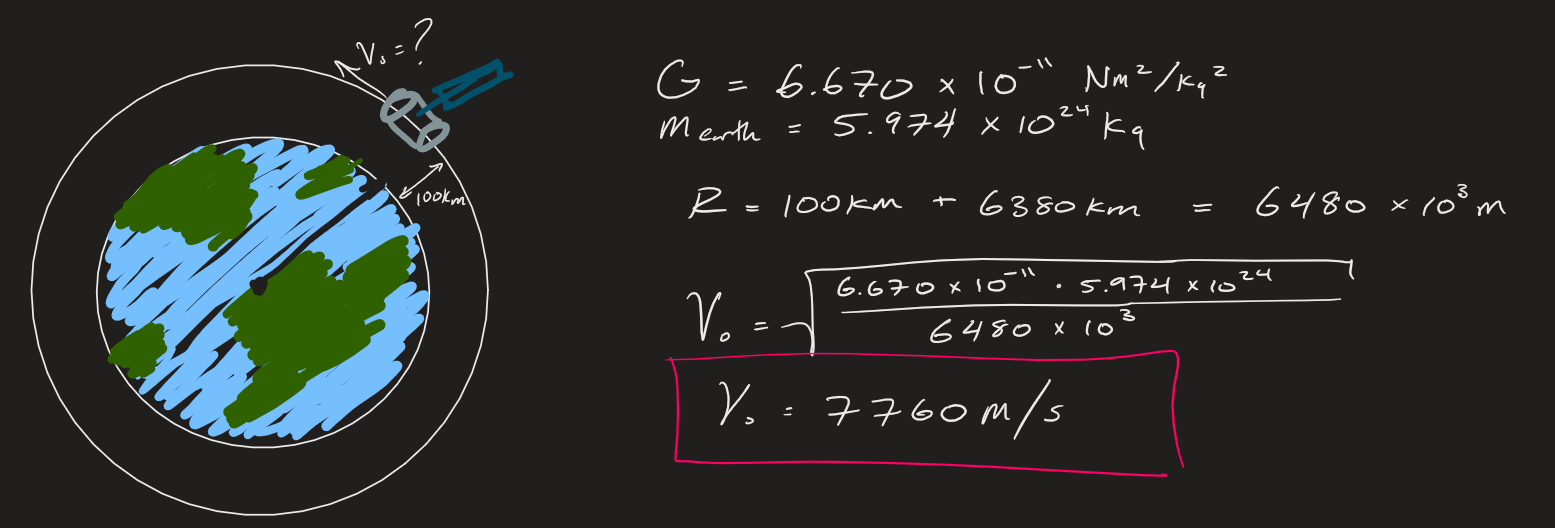L2: Motion in Space
Impulse
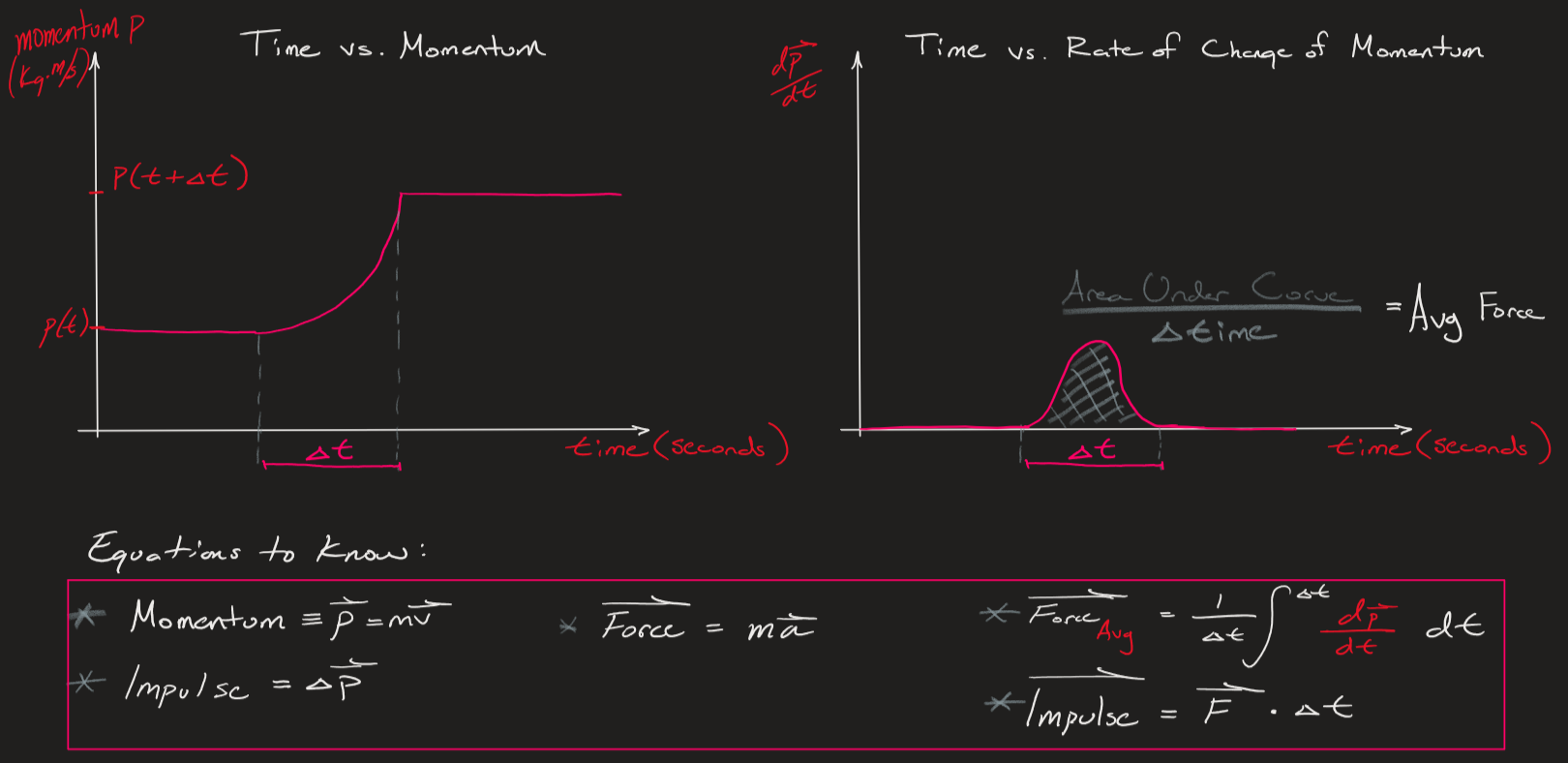
One of the most fundamental concepts we will be constantly talking about in this series is the idea of Impulse. Impulse simply a change in momentum. Given the momentum of an object a t1 and a the momentum of the object at t2 the difference between these two momentum is equal to the Impulse.
One of the most fundamental concepts we will be constantly talking about in this series is the idea of Impulse. Impulse simply a change in momentum. Given the momentum of an object a t1 and a the momentum of the object at t2 the difference between these two momentum is equal to the Impulse.
As shown in the time vs. momentum graph above you can see that when a change in momentum occurs over a specific period of time, we can characterize this as an impulse. If we take the integral of the change in momentum and divide it by the change in time we get the average Force applied on the object. Thus, the integral of the change in momentum is equal to the instantaneous force applied. The impulse is therefore equal to the force multiplied by the change in time the force is applied over.
Newton's Universal Law of Gravitation
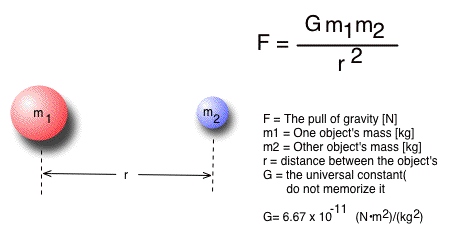
As described in the previous lecture, Newton theorized that the gravitational force enacted on one body by another body could be formulated by the following equation:
As described in the previous lecture, Newton theorized that the gravitational force enacted on one body by another body could be formulated by the following equation:
It is important to note that Gravity is considered a Weak Force compared to other forces in Physics. To put this in perspective, consider the real world example of the Satellite named Rosetta. The mission of Rosetta was to study asteroids located between Mars and Jupiter. At one point Rosetta was studying an Asteroid by the name of Steinz was at a distance of 800km away. Try to calculate the magnitude of Force the Asteroid had on the satellite:
Given:
Given:
- Mrosetta = 500 kg
- Masteroid = 1.208 x 10^11 kg
- r = 800km = 800 x 10^3 m
- F = (G) x (Mrosetta) x (Masteroid) / (r)^2 = (6.67 x 10^-11) x (1.208 x 10^11) x (500) / (800 x 10^3) = 10^-6 Newtons = 10 uN
Considering the scale of these two bodies one might expect a much larger force, but this is not the case. However, if we imagine a case where one body was much larger this force could potentially be much higher.
On Earth, most of our calculations in gravity tend to boil down to a simpler equation:
On Earth, most of our calculations in gravity tend to boil down to a simpler equation:
F = m x g where g = 9.81 m/s^2
But have you ever considered where this gravitational constant g comes from? It is actually derived from Newton's Universal Law of Gravity! By setting the mass of Earth as m1, the radius of Earth as r. The equation simplifies to the equation above. Also keep in mind that Newton's Universal Law of Gravity breaks down for bodies that move at very high velocities, that near the speed of light.
Frames of Reference
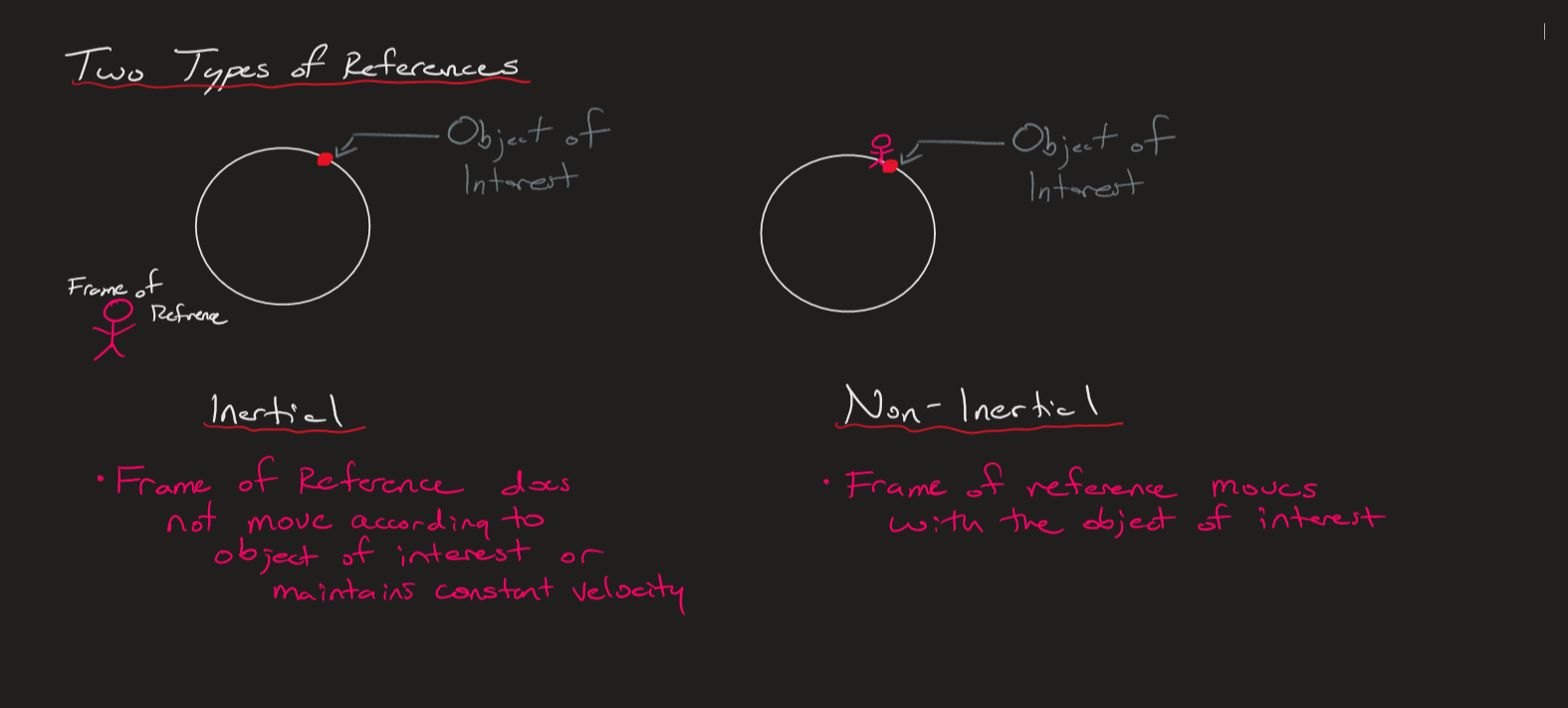
In order us to be able to observe the change in velocity of another object, we must have a reference object that is either stationary or moves at a constant velocity. This reference object is known as an Inertial Frame of Reference. For example, if I am sitting on the ground and I am observing the speed of a car traveling 60 mph, I would then say the speed of the car is 60mph in reference to my stationary inertial frame of reference. However, if I am in a car driving 60mph next to the other car also driving 60mph, it would seeem as if the car was stationary in reference to my constant velocity frame of reference. It is only in two forms of reference in which our frame of reference is independent of the motion of the observed object. In cases where the frame of reference is moving at a non-constant velocity, the motion of the observed object is dependent on the inertial frame of reference. Almost all Engineering problems require a frame of reference.
In order us to be able to observe the change in velocity of another object, we must have a reference object that is either stationary or moves at a constant velocity. This reference object is known as an Inertial Frame of Reference. For example, if I am sitting on the ground and I am observing the speed of a car traveling 60 mph, I would then say the speed of the car is 60mph in reference to my stationary inertial frame of reference. However, if I am in a car driving 60mph next to the other car also driving 60mph, it would seeem as if the car was stationary in reference to my constant velocity frame of reference. It is only in two forms of reference in which our frame of reference is independent of the motion of the observed object. In cases where the frame of reference is moving at a non-constant velocity, the motion of the observed object is dependent on the inertial frame of reference. Almost all Engineering problems require a frame of reference.
Centripetal and Centrifugal Forces
The image above shows a common circus entertainment event in which a person riding a motorcycle is able to driving constantly around the inside of the sphere following a circular path. How is this possible? Why does the person not fall while at the top? The answer: Centripetal and Centrifugal forces which govern circular motion. Let's take a deeper look into what we mean. We will describe everything from a non-inertial frame of reference as shown below:
We are interested in formulating the equations that govern the motion of a rotating body in reference to rotating frame:
Calculating Orbital Velocity
The orbital velocity is the velocity required to maintain the given altitude orbit. Here is how to calculate this value:
The orbital velocity is the velocity required to maintain the given altitude orbit. Here is how to calculate this value:
Example #1:
Let's attempt to calculate the required orbital velocity to maintain an orbit 100km from the surface of the Earth:
Let's attempt to calculate the required orbital velocity to maintain an orbit 100km from the surface of the Earth:
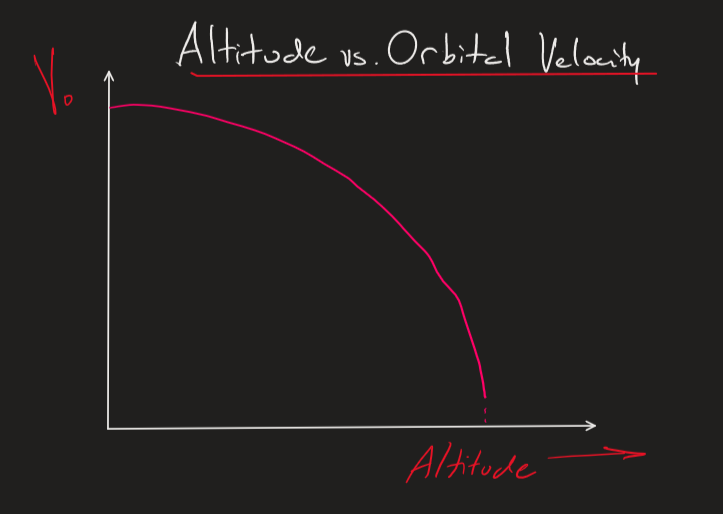
It is important to note that as you increase the distance from Earth the orbital velocity continues to decrease until you are infinitely far away and the orbital velocity nears zero, as shown in the graph below.
Now that you understand how to find orbital velocity requirements, this will be key in understanding how to generate the requirements of a rocket.