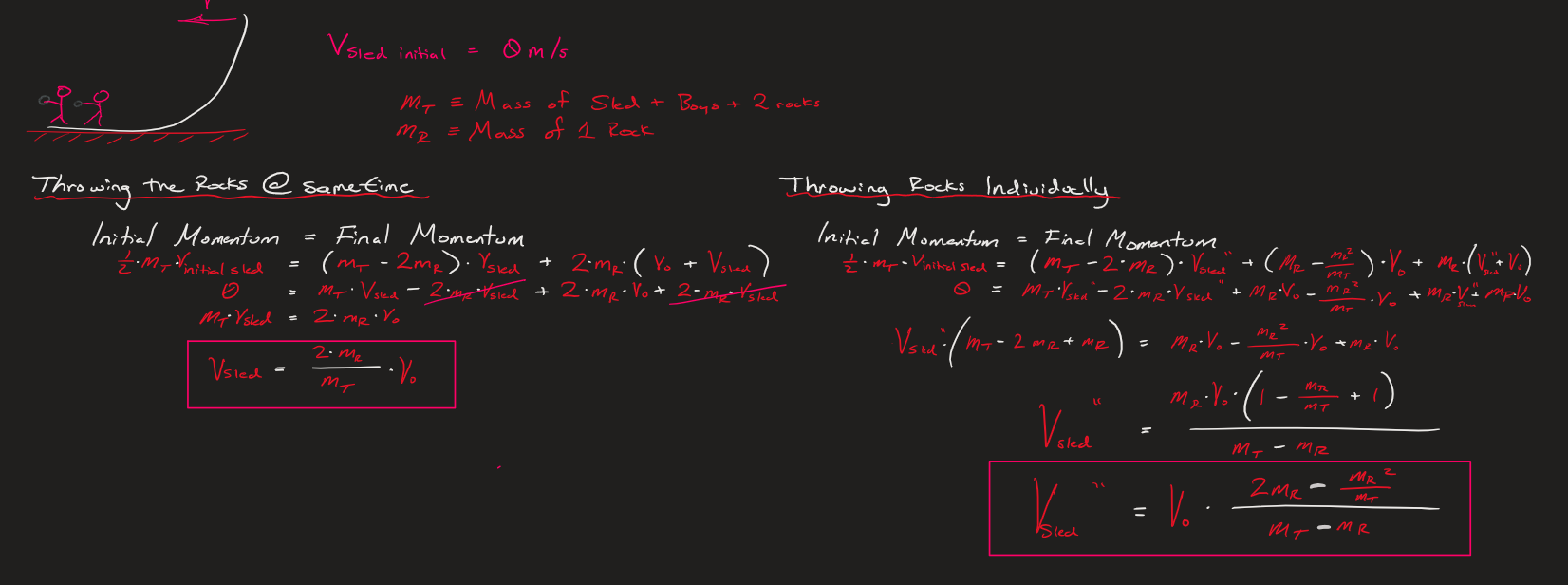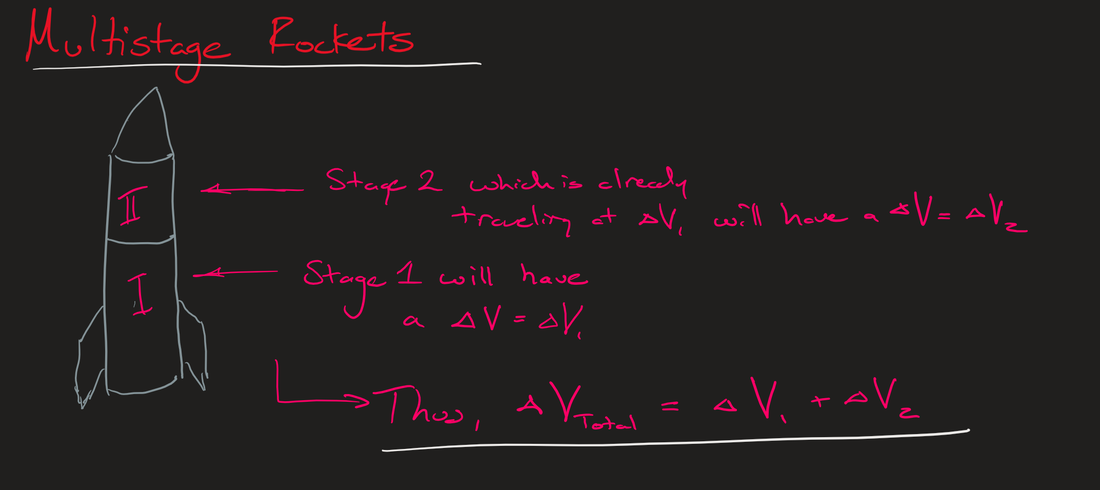L4: The Rocket Equation
Analogy
Let's start with a large scale analogy to how rocket propulsion works. Let's say two boys are standing on a sled with 2 rocks in their hands and the sled initially is not moving. They decide to try two methods to move them forward. The first way is where both boys throw their rocks at the same time away from them. The second way is to first throw the first boy's rock, then moments later have the second boy throw his rock. The boys find that method two actually generated a higher change in velocity for the sled. We can prove this by using some conservation of momentum equations as seem below:
Let's start with a large scale analogy to how rocket propulsion works. Let's say two boys are standing on a sled with 2 rocks in their hands and the sled initially is not moving. They decide to try two methods to move them forward. The first way is where both boys throw their rocks at the same time away from them. The second way is to first throw the first boy's rock, then moments later have the second boy throw his rock. The boys find that method two actually generated a higher change in velocity for the sled. We can prove this by using some conservation of momentum equations as seem below:
From the calculations above you can see that the end velocity of Throwing the rocks individually resulted in a higher end velocity than simply throwing both rocks out at the same time. This analogy is similar to how rocket engines work, in that the individual ejected particles are what make up the overall change in momentum of the vehicle.
The Rocket Equation
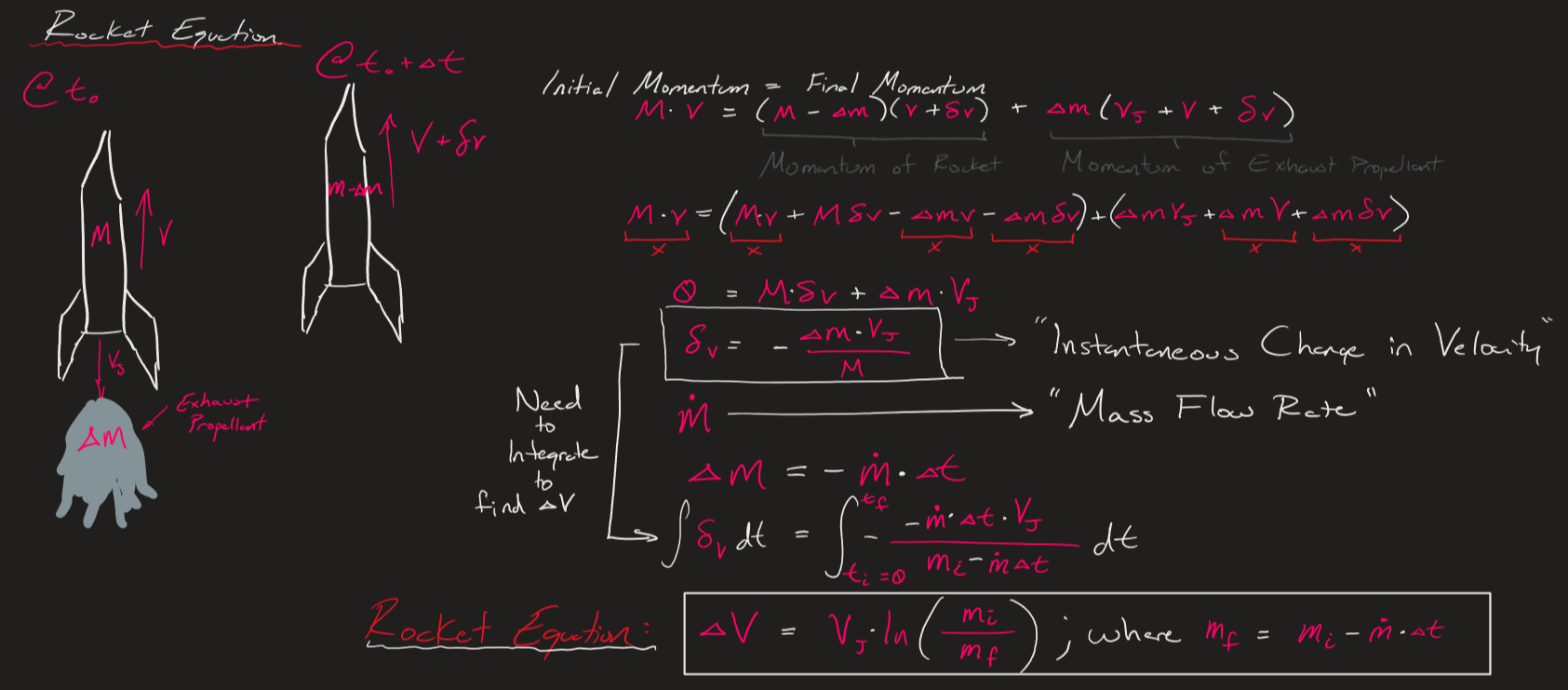
In 1903 a Russian school teacher by the name of Tsialkowski formed the most fundamental equation used for sizing rockets. This so called Rocket Equation or Tsialkowski Equation forms the basis of understanding the cyclic problem of adding more fuel in attempting to yield a higher altitude. We will derive Tsialkowski's Equation by starting with conservation of momentum equations as seen below. The equations below are calculated at two points in a rocket's flight, an instantaneous point where the rocket it traveling upward and is exhausting out propellant, and another point delta t after:
In 1903 a Russian school teacher by the name of Tsialkowski formed the most fundamental equation used for sizing rockets. This so called Rocket Equation or Tsialkowski Equation forms the basis of understanding the cyclic problem of adding more fuel in attempting to yield a higher altitude. We will derive Tsialkowski's Equation by starting with conservation of momentum equations as seen below. The equations below are calculated at two points in a rocket's flight, an instantaneous point where the rocket it traveling upward and is exhausting out propellant, and another point delta t after:
From the rocket equation we derived above we can use it to calculate the change in velocity the rocket will be able to achieve knowing your exit exhaust velocity (Vj), your initial mass(mi), and your final mass(mf). We will get into calculating exhaust velocity later in our tutorial series. It is important to note that this equation does not take into factors of aerodynamic resistance and the force of gravity, and for that reason we call it the "Ideal Velocity Increment". Now let's talk about figuring out initial and final mass values, which makes up our rocket's Mass Ratio.
Mass Ratio = mfinal / minitial
In order to get a high ΔV we either need a large Vj value or a large (mi/mf). We will later find out there are limitations to how large we can make our vj in later chapters, which is limited to 3000-5000 m/s. So the best way to change delta v is have a small Mass Ratio. So let's look closer at what the mass of a rocket is composed of:
mi = mu [Useful/Payload] + ms [Structure] + mp [Propellant]
mf = mu [Useful/Payload] + ms [Structure]
mf = mu [Useful/Payload] + ms [Structure]
Let's take this mass composition further and separate each part into a mass fraction:
- α = mu / mi
- β = ms / mi
- γ = mp / mi
- Thus, α + β + γ = 1
From this mass fraction we can simplify the Rocket equation into the following:
ΔV = Vj x ln( 1 / α + β )
Thus, from the equation above. If we solve for the mass fraction of either the Useful/Payload or the Structural we get the following equations:
α = e^( -ΔV / Vj ) - β
β = e^( -ΔV / Vj ) - α
β = e^( -ΔV / Vj ) - α
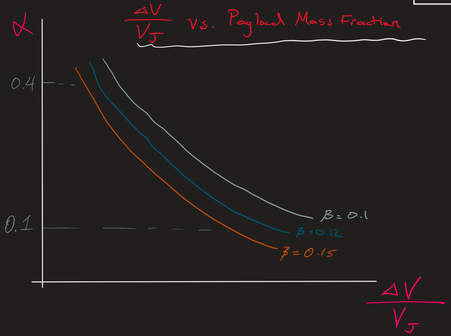
Keep in mind when solving these equations we need the delta V to be in the order of 3,000 to 5,000 m/s. If we form a graph for different values of β here is what we find:
|
From what is seen here. If we want to have a high Payload mass fraction then we need to have a light weight structure. If I have a high value Vj then I can have a higher value for the Payload Mass fraction, or I have a rocket which requires a higher ideal velocity then must take a lower Payload Mass fraction. This makes up the fundamental construct of how the rocket equation works. If you want a higher payload mass either you will need a lighter structure or a higher Vj which we will later see can be calculated later on.
|
Rocket Staging
The problem we will encounter as we wish to get into Vt which are in the order of 10 to 12 km/s it is very difficult to have a single rocket which achieves this ΔV. So far it has been impossible for the "single rocket to orbit" to take shape. This is primarily due to the fact that the structural mass of the rocket will stay constant as propellant is used up, which if all the propellant is used up then why should we keep this excess structural mass needed to contain the propellant? This is where rocket staging comes into play. As sections of the rocket are used up (ie. the Structural Mass for the rocket engine), then we should jettison that stage and continue on with another rocket engine that without the old weight is now lighter and performs much better. Take a look at how ΔV changes:
The problem we will encounter as we wish to get into Vt which are in the order of 10 to 12 km/s it is very difficult to have a single rocket which achieves this ΔV. So far it has been impossible for the "single rocket to orbit" to take shape. This is primarily due to the fact that the structural mass of the rocket will stay constant as propellant is used up, which if all the propellant is used up then why should we keep this excess structural mass needed to contain the propellant? This is where rocket staging comes into play. As sections of the rocket are used up (ie. the Structural Mass for the rocket engine), then we should jettison that stage and continue on with another rocket engine that without the old weight is now lighter and performs much better. Take a look at how ΔV changes:
So form this we can see that the rocket equation changes just a bit with multistage rocket like this:
- Mi1 = Inital Mass of Rocket with 1st stage and above
- Mb1 = Burn out Mass of the Rocket with 1st stage and above (All propellant has been used up)
- Mi2 = Inital Mass of Rocket with 2nd stage and above
- Mb2 = Burn out Mass of the Rocket with 2nd stage and above (All propellant has been used up)
- ...
ΔV = Vj1 x ln( Mi1 / Mb1 ) + Vj2 x ln( Mi2 / Mb2 ) + ...
As a consequence of staging the initial stages will need to support a larger weight from above, thus we may require more thrust. So we may need to add additional rockets to the initial stage, this is known as "clustering".