L3: Orbital Requirements
Now that we understand how objects orbit around planets, we can now use some equations to figure out the total energy required to put a rocket into a particular orbit. Before we do that, let's talk a bit about the different types of orbits, and what distinguishes each from the others.
Types of Orbits
As we discussed in the previous lecture we can use an non-inertial frame of reference to define the circular motion around a planet by using a pseudo force known as a "centrifugal" force. This force is used to balance out the force of attraction that the planet has on the orbiting body, from this balance, we were then able to solve for angular velocity. From the angular velocity we were able to come up with the orbital velocity of the orbiting body, which is the velocity the body will be traveling at that particular height above the planet.
To start to differentiate the different types of orbit, it is easier to understand each if we translate the orbital velocity of the body at a particular height to the period of the orbit, which is the total time it takes to complete a full orbit.
Types of Orbits
As we discussed in the previous lecture we can use an non-inertial frame of reference to define the circular motion around a planet by using a pseudo force known as a "centrifugal" force. This force is used to balance out the force of attraction that the planet has on the orbiting body, from this balance, we were then able to solve for angular velocity. From the angular velocity we were able to come up with the orbital velocity of the orbiting body, which is the velocity the body will be traveling at that particular height above the planet.
To start to differentiate the different types of orbit, it is easier to understand each if we translate the orbital velocity of the body at a particular height to the period of the orbit, which is the total time it takes to complete a full orbit.
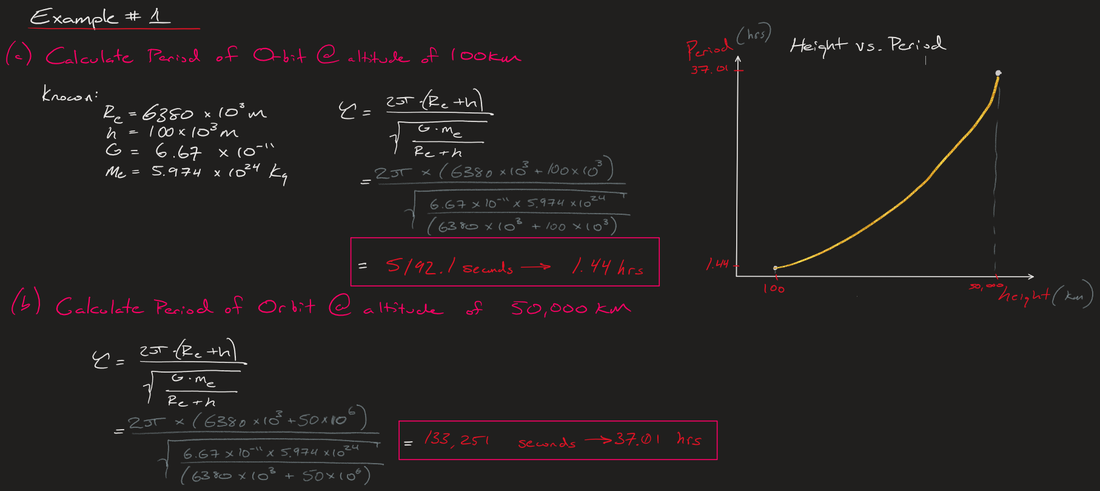
From the calculations above you can see how to come up with the Period of Rotation. This period will be what distinguishes most of the orbits we will be talking about. Let's do some examples with our new equations:
Example #1 : (Attempt this yourself before looking at the solution below)
(a) Calculate the Period of Orbit at 100km above Earth's surface
(b) Calculate the Period of Orbit at 50,000km above Earth's surface
Example #1 : (Attempt this yourself before looking at the solution below)
(a) Calculate the Period of Orbit at 100km above Earth's surface
(b) Calculate the Period of Orbit at 50,000km above Earth's surface
There are actually two different values we define for the period of Earth's rotation:
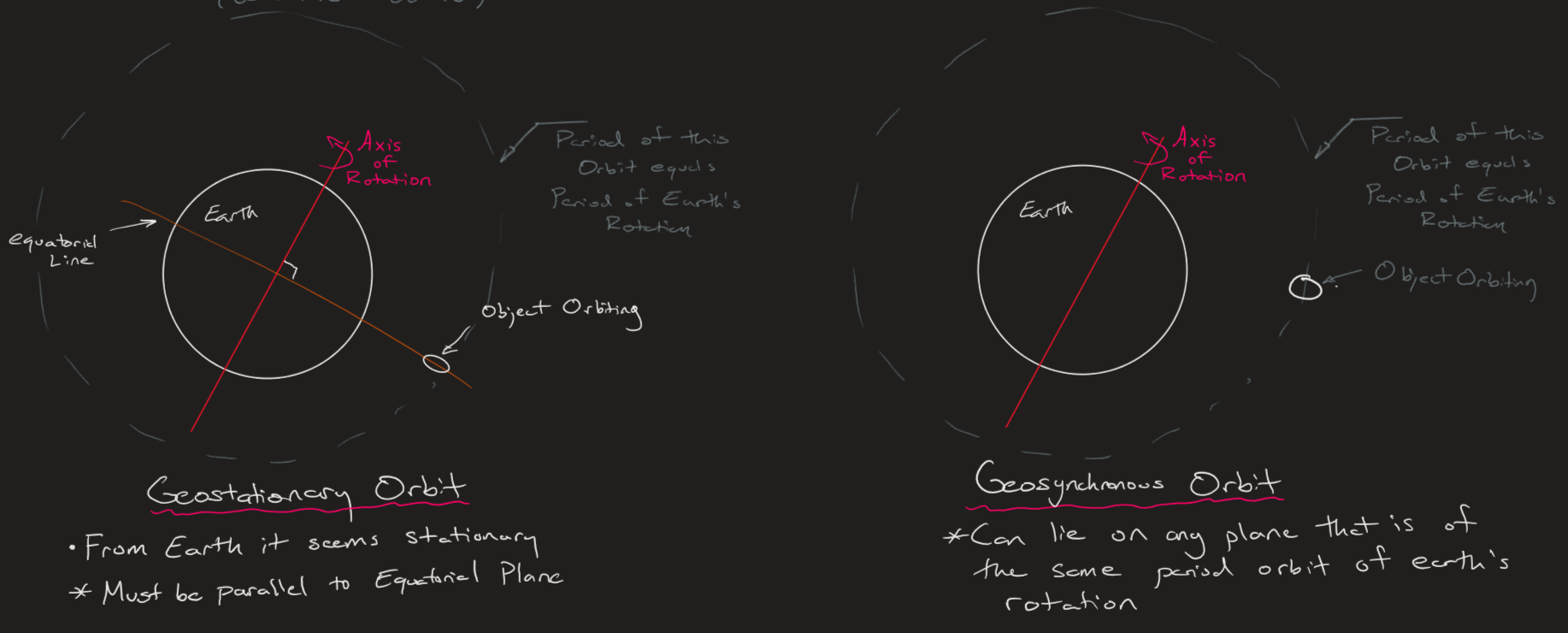
Here are a few orbits of interest:
- Solar Day
- This is more so an approximation to the actual value, that humans define which is 24 hrs.
- Sidereal Day
- This is the actual value of time it takes for a full rotation, which is 23 hrs, 56 min, 41 sec.
Here are a few orbits of interest:
- Geostationary Orbit (Clarke Orbit)
- This is an orbit which runs exactly parallel to the equatorial line around Earth and has a period equivalent to the period of Earth's rotation. What makes it special is that from the observation reference of Earth, this body stays at a fixed location.
- Geosynchronous Orbit
- This is an orbit similar to the Geostationary, but is not constrained to being parallel to the equatorial line around Earth. This however means that is does not look to be at a fixed location, but does have the same period of orbit as the period of Earth's rotation. It may be a bit hard to picture in your head why this doesn't seem to stay in a fixed location, but think about the Earth's tilted axis as it rotates.
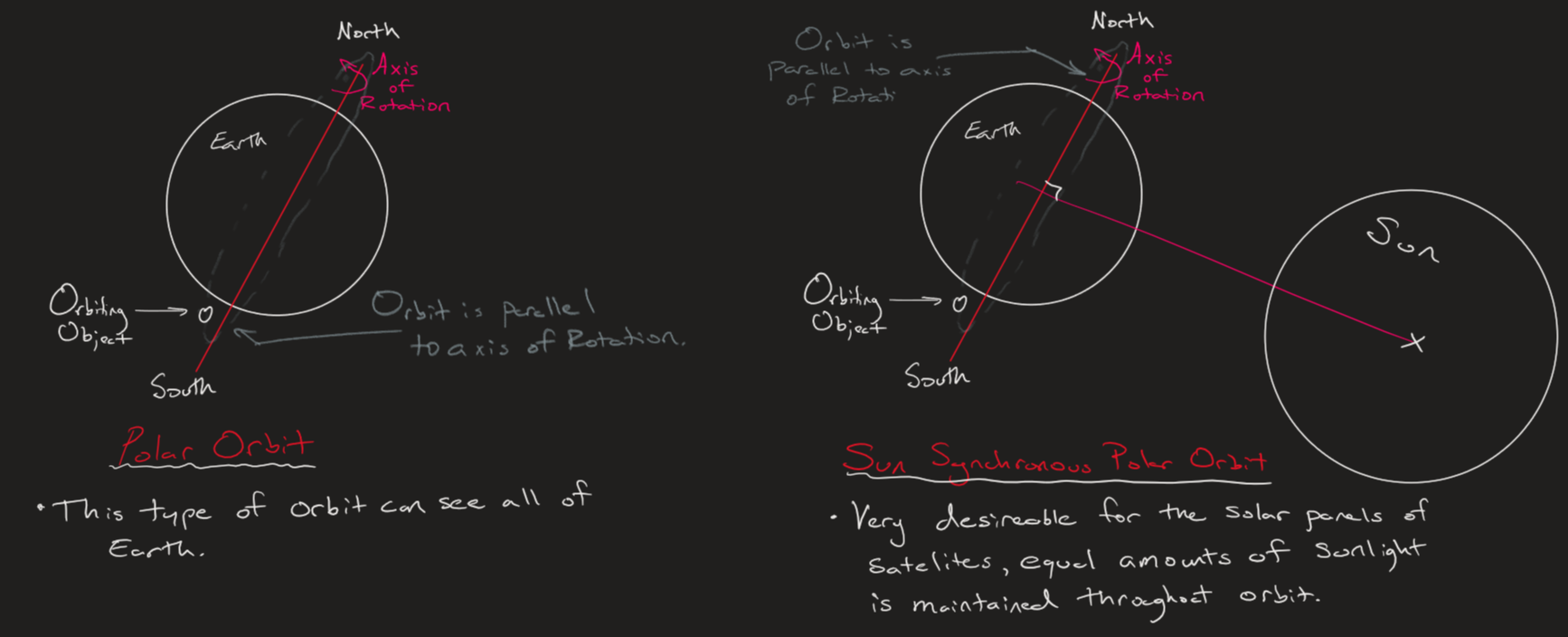
- Polar Orbit
- This is an orbit which runs exactly parallel to Earth's axis of rotation, giving the advantage of the satellite being able to view all of the Earth.
- Sun Synchronous Polar Orbit
- This is the same as the Polar orbit except angle between a line running from the center of the Sun and the Earth must be perpendicular to the axis of rotation. This will allow the sunlight from the sun to be equal all throughout the orbit of the satellite.
- Low Earth Orbit (LEO)
- Mainly used for scientific studies. Takes place in the higher portions of the atmosphere (altitude greater than 320km), where the air resistance is not enough to bring it down in altitude. Total Altitude Range is 320 - 1100 km.
- Medium Earth Orbit (MEO)
- Most commonly used for GPS/Navigation satellites. Is the region above LEO and below Geostationary Orbit. Total Altitude Range is 8,000 to 12,000km.
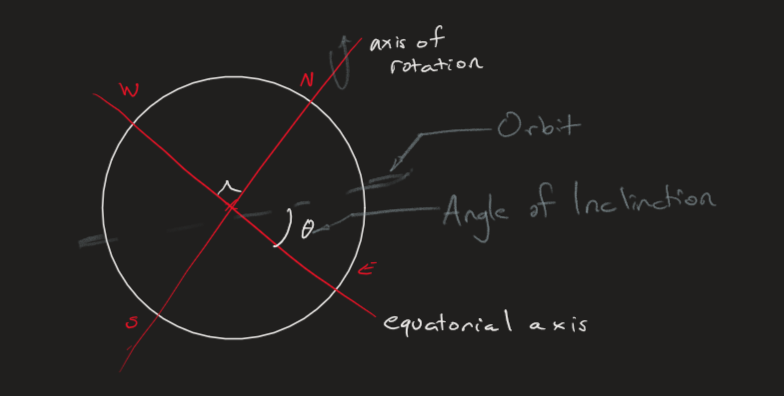
Angle of Inclination
Not all orbits have to be parallel or perpendicular to a special axis of the planet of interest. The way we measure this angle offset is relative to the axis perpendicular to the axis of rotation. This angle offset is known as the angle of inclination as shown below:
Not all orbits have to be parallel or perpendicular to a special axis of the planet of interest. The way we measure this angle offset is relative to the axis perpendicular to the axis of rotation. This angle offset is known as the angle of inclination as shown below:
Elliptical vs Circular Orbits
From what we discussed from the Planets orbiting the Sun we described that they orbited in an Elliptical Orbit. But when describing satellites orbiting the Earth we discussed them taking Circular orbits? All orbits are considered Elliptical, but for the most part are almost identical to a circular orbit which is a special type of Ellipse in which the distance between the foci is zero. If we were to consider orbits to be perfectly circular we would violate this rule in the case where any sort of force (ie. a asteroid hitting the planet, or another Planet getting close) could pull the planet out of its normally circular orbit. Thus we categorize all orbits as Elliptical.
From what we discussed from the Planets orbiting the Sun we described that they orbited in an Elliptical Orbit. But when describing satellites orbiting the Earth we discussed them taking Circular orbits? All orbits are considered Elliptical, but for the most part are almost identical to a circular orbit which is a special type of Ellipse in which the distance between the foci is zero. If we were to consider orbits to be perfectly circular we would violate this rule in the case where any sort of force (ie. a asteroid hitting the planet, or another Planet getting close) could pull the planet out of its normally circular orbit. Thus we categorize all orbits as Elliptical.
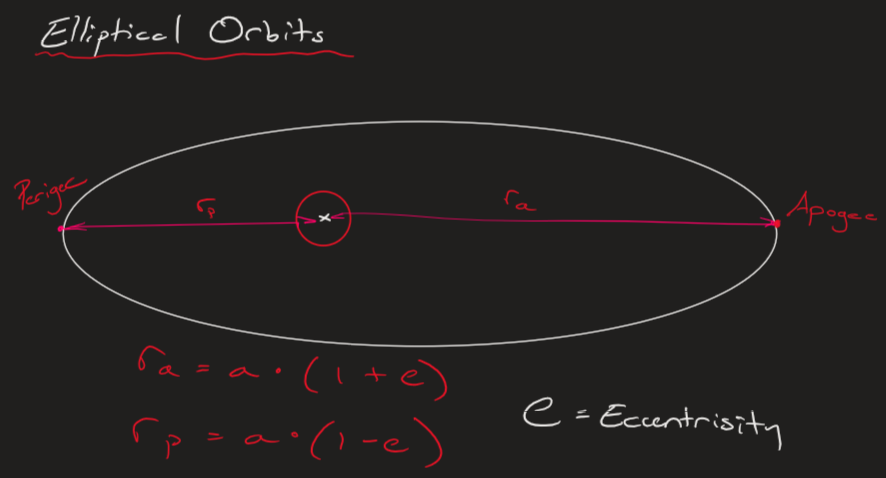
We discuss a parameter of an Ellipse known as eccentricity, which is a value ranging from 0 and 1 which describes how much the ellipse looks like a circular orbit (ie. eccentricity of zero) or like an unbounded ellipse (ie. eccentricity of 1).
Elliptical Orbits have two very important points in which the distance from the first focus is smallest, known as the perigee, and the farthest distance from the first focus is known as the apogee. The perigee and apogee distances are directly related to the eccentricity, as seen below:
Elliptical Orbits have two very important points in which the distance from the first focus is smallest, known as the perigee, and the farthest distance from the first focus is known as the apogee. The perigee and apogee distances are directly related to the eccentricity, as seen below:
Total Velocity
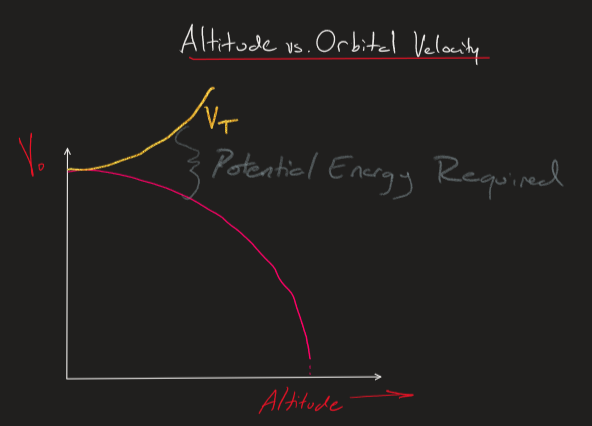
So far we have discussed the orbital velocity. But when we describe the Total velocity we are adding both the velocity required to go from the surface of the Earth and the orbital velocity. Let's solve this in parts:
So far we have discussed the orbital velocity. But when we describe the Total velocity we are adding both the velocity required to go from the surface of the Earth and the orbital velocity. Let's solve this in parts:
- What is the total work required to take the spacecraft from Radius of Earth to the Radius of Earth + the target altitude?
|
So what have we found from the total velocity? We have found that even though the orbital velocity decreases as the altitude increases. The total velocity continues to increase since the velocity required to go from the earth surface to the specific altitude becomes significantly larger as the altitude increases.
This total velocity is what we will need to know in order to size our rocket and its rocket engine! We will go into the requirements and propulsion theory in the next tutorial. |
Calculating Escape Velocity
We define Escape Velocity as the velocity required to exit Earth's gravitational force. You can see how we do the calculation below:
We define Escape Velocity as the velocity required to exit Earth's gravitational force. You can see how we do the calculation below:
Final Practical Orbital Example
Sir Richard Brandson, the CEO of Virgin Orbit is designing a air launch system that uses a high speed plane with a rocket attached to it, so that when it reaches an altitude of around 10-15km, then you launch the rocket. What is the value of the velocity needed to take the rocket from 5km to 100km orbit?
Sir Richard Brandson, the CEO of Virgin Orbit is designing a air launch system that uses a high speed plane with a rocket attached to it, so that when it reaches an altitude of around 10-15km, then you launch the rocket. What is the value of the velocity needed to take the rocket from 5km to 100km orbit?
From what you can see above 1.278 km/s is the needed velocity our rocket needs to get to in order to reach the 100km orbit. But if you were to compare this value with the value you get if you started on Earth's surface, you would find that this velocity does not change by much. Thus, it is not very advantageous to perform an air launch? While the total velocity may not have changed much, there is an orbital velocity component that is given to the rocket which will gives an advantage to sizing a smaller rocket.